Calculadora de Juros Compostos
Os juros compostos crescem exponencialmente porque são sempre calculados sobre o valor anterior. Use nossa calculadora de juros compostos para fazer cálculos financeiros de maneira fácil e simples!
Simulação descontando Imposto Renda
Como usar a calculadora de juros compostos
- Preencha o campo de valor inicial;
- Preencha o campo de valor mensal;
- Preencha a taxa de juros anual ou mensal;
- Preencha o campo de período por meses ou anos;
- Se preferir descontar Imposto de Renda basta selecionar a alíquota por período (se não, deixe sem preencher);
- Clique em calcular e veja o resultado.
Viu como é fácil? Agora é só usar nossa calculadora de juros compostos para simular.
Continua depois da publicidade
Navegue pelo conteúdo
Como funciona a fórmula de juros compostos?
Utilizamos essa fórmula para calcular os juros compostos ou mais conhecido como juros sobre juros:
A = P (1 + i) ^ t
Para melhorar para você, vamos explicar cada variável da fórmula:
- A = valor final, ou seja, o resultado da conta;
- P = valor inicial depositado;
- i = taxa de juros;
- t = tempo do investimento.
Um ponto importante, é que a taxa de juros e o tempo devem estar na mesma unidade.
Para facilitar, vamos te dar um exemplo:
Se você quer usar a fórmula para simular um investimento que rende 0,5% ao mês, na fórmula você deve usar os períodos mensais, ou seja, se você quer simular 10 anos nessa taxa, então utilize 10×12 que são 120 no campo t.
Pode parecer um desafio entender juros compostos, mas fique tranquilo, vamos te ajudar de forma mais simplificada:
Então, suponhamos que você investisse R$ 15.000,00 a uma taxa de 10% ao ano durante 5 anos.
No primeiro ano você teria um rendimento de 10% que seria igual a R$ 1.500,00, totalizando assim um valor de R$16.500,00.
Já no segundo ano de investimento, você teria um rendimento de 10% do valor de R$ 16.500,00 e não mais do valor inicial, o valor do rendimento seria no segundo ano R$ 1.650,00.
Totalizando assim no final do segundo ano um valor de R$ 18.150,00. Portanto, o valor do rendimento será sempre 10% do valor do último período e não em cima do valor inicial do investimento, criando um efeito exponencial do juros sobre juros.
No final você teria o valor de R$ 24.157,65.
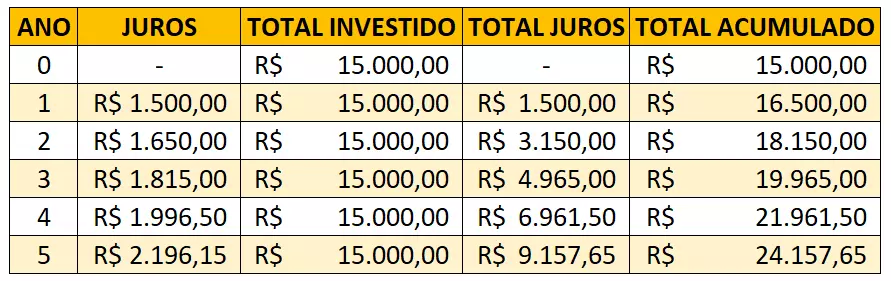
Perceba que a cada ano, o valor ganho em juros aumenta mesmo sem nenhum novo depósito de dinheiro. Já no juros simples, o juros incide somente no valor inicial.
Para você ter uma ideia, o total que você teria se essa conta fosse feita em juros simples, seria de R$ 22.500,00. Ou seja, uma diferença de R$ 1.657,65 graças ao poder exponencial dos juros compostos.
O que são juros compostos?
Os juros compostos são a prática de juros sobre juros. Na maioria das vezes podemos dizer, eles são mais utilizados no sistema financeiro, pois conseguem oferecer maiores retornos nos investimentos se compararmos aos juros simples.
Algo que pode ser considerado um fato sobre os juros compostos; eles fazem parte do conceito mais importante que você precisa aprender e dominar sobre o mundo dos investimentos.
O conceito básico de um bom planejamento financeiro pessoal são os juros, geralmente esse conceito é dominado pelos investidores que buscam maiores retornos nos investimentos e na construção de patrimônio.
O maior problema é que existe uma tendência das pessoas subestimarem a forma dos juros trabalhar com o dinheiro e acabam se perdendo na hora de investir.
Esse exemplo vai te ajudar melhor. Tente se imaginar nessa situação: você vai pegar um dinheiro emprestado com seu amigo.
Mas seu amigo cria uma condição para emprestar a você, que é de devolver o dinheiro somado de um determinado valor.
Esse valor extra que você irá pagar para o seu amigo, é o famoso juros.
Em simples palavras, o juro é a remuneração paga pelo empréstimo de algum valor em dinheiro.
Mesmo parecendo muito simples, tem muita gente quebrando a cabeça e se confundindo quanto ao assunto.
Entender bem esse conceito vai te ajudar na hora de analisar o retorno dos seus investimentos ao longo do tempo, isso é fundamental no universo das finanças.
Juros simples e juros compostos
No regime de juros simples, o percentual de juros (ou taxa) se aplica apenas sobre o valor inicial. Significa que a remuneração sobre o dinheiro só incidirá sobre o valor investido ou emprestado no início.
Conheça as principais diferenças entre os juros simples e os juros compostos:
Juros simples
- São pagos mensalmente ou anualmente ao credor;
- São iguais ao longo do tempo, mas reduzem em termos reais (efeito dado o impacto da inflação);
- Somados nominalmente ao capital, formam uma reta (ex.: 1000, 1100, 1200 etc.);
- São como os frutos de uma árvore: são colhidos e consumidos;
- Tecnicamente, ocorre a fruição imediata dos juros pelo credor;
- Se não pagos e não incorporados ao montante, gera perda inflacionária e da porcentagem de rendimento.
Juros compostos
- São pagos ao credor somente no vencimento;
- São crescentes no tempo em termos reais e nominais, se a taxa for maior que a inflação;
- Incorporados ao capital formam uma curva ascendente. (ex.: 1000, 1100, 1210 etc.);
- Tecnicamente, ocorre a fruição diferida dos juros pelo credor;
- Se pagos, não incorporam ao montante, que não cresce durante o período em que forem pagos;
- Quanto maior o tempo, mais exponencial é o retorno.
Juros compostos pode ser definido como a aplicação de juros sobre juros, ou seja, os juros compostos são aplicados ao montante de cada período.
O poder dos juros sobre juros
Depois de aprender a calcular os juros compostos com nossa calculadora de juros compostos, agora é a hora de ver o poder transformador que esses juros sobre juros podem fazer a seu favor em seus investimentos e como eles podem te enriquecer rapidamente.
Repare na imagem abaixo:
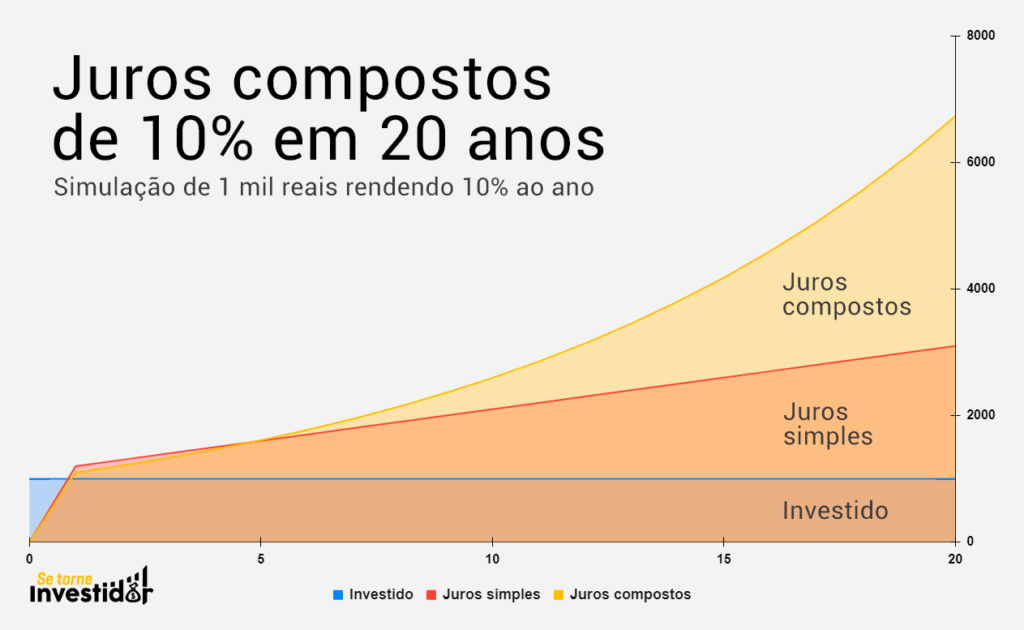
Como você pode ter visto, no longo prazo (mais de 15 anos) é onde você vai colher os maiores frutos dos juros compostos.
Então comece a brincar com nossa calculadora de juros compostos e faça várias simulações.
Como dizia o mestre Albert Einstein:
“Os juros compostos são a força mais poderosa do universo e a maior invenção da humanidade, porque permitem uma confiável e sistemática acumulação de riqueza”
Albert Einstein
Como funciona o Imposto de Renda para investimentos de renda fixa?
Neste sentido, para fazer a declaração dos investimentos do imposto de renda para renda fixa basta ir à sessão “Bens e Direitos” e informar o valor em reais que você investiu.
Contudo, para informar os rendimentos advindos da renda fixa deverá ir à sessão ”Rendimentos Sujeitos à Tributação Exclusiva/Definitiva” e escolher o item “Rendimento de aplicação financeira”. Em suma, todos os investimentos em renda fixa devem seguir o mesmo sistema de tributação.
Valores da Alíquota
Nesse sentido, eles são sujeitos a uma tabela regressiva de Imposto de Renda, visto que as alíquotas irão diminuir conforme o prazo do investimento. Portanto, a alíquota mais alta é de 22,5% para aplicações mantidas até seis meses. Caso tenha mais de seis meses a um ano, irá cair para 20%. Investimentos com mais de dois anos será de 17,5%, para mais de dois anos a alíquota será de 15%.
- Até 180 dias: 22,5%
- 181 a 360 dias: 20%
- 361 a 720 dias: 17,5%
- acima de 720 dias: 15%
De um modo prático, se você investir R$ 1000 em uma renda fixa durante 365 dias, a rentabilidade total neste período é de R$ 1.100. Ou seja, a aplicação rendeu durante este período R$ 100, assim a alíquota é de 17,5% o que dá R$ 17,50 em impostos.
Contudo, essa tributação vale para CDBs, fundos, debêntures e vários outros investimentos de renda fixa. Entretanto, fique atento, pois existem algumas exceções e especificações em relação a alguns investimentos de renda fixa. Devido à isenção do imposto de renda, como a poupança, LCI e LCA. No entanto, vale ressaltar que mesmo que alguns produtos sejam isentos de cobrança do imposto de renda, o investidor ainda precisa declarar.
Uma vez que a Receita Federal precisa saber dos investimentos que tem na carteira e evitar que caia na malha fina. A alíquota do imposto de renda para investidores é alta principalmente para resgates de curto prazo. Deste modo, com uma tabela regressiva de impostos, quanto maior o prazo de resgate, menos impostos será pago para receita federal.
IOF
O Imposto sobre Operações Financeiras (IOF), também recai em alguns investimentos de renda fixa, contudo naqueles de curtíssimo prazo, como os de menos de 30 dias. Portanto, a base de cálculo do IOF ele recai apenas em cima dos lucros da aplicação, e também segue uma tabela de alíquotas decrescentes.
Ativos resgatados até o dia, por exemplo, a cobrança é de 96% sobre os juros obtidos; até 15 dias cai para 50%, depois de 29 dias a cobrança irá cair bastante pagando apenas 3% e chegando até o, 30° dia será 0%. No site da Receita Federal o contribuinte poderá verificar a tabela completa.
Sobre o autor
Wesley Martins
Perguntas frequentes
Juros compostos são um regime de capitalização em que os juros de um período incidem sobre o valor acumulado do período anterior.
Como o período anterior já está acrescido de juros, então esse regime também é conhecido popularmente por “juros sobre juros”.
A diferença principal entre esses dois regimes é a base em que há incidência da taxa de juros.
Enquanto nos juros simples os juros sempre incidem sobre o valor inicialmente investido, nos juros compostos há incidência sobre o valor acumulado até o período imediatamente anterior.
Atualmente, todas as operações em que há incidência de juros rendem de acordo com o regime de juros compostos.
Nesse sentido, você encontrará aplicações de juros compostos nos investimentos de renda fixa, em empréstimos e financiamentos.
Vamos supor que você está indo ao banco solicitar um empréstimo pessoal no valor de R$ 10.000,00.
Durante a solicitação, o gerente do seu banco diz que você poderá pagar esse empréstimo em 24 meses a uma taxa de 3% ao mês.
Para descobrir quanto você irá pagar na real das contas, basta fazer assim:
Utilizando a fórmula de juros compostos, teremos:
A = 10.000 (1 + 3%)^24
Ao fazer esse cálculo no Simulador de Juros Compostos, você encontrará o montante final de R$ 20.327,94, ou seja, você iria pagar R$ 10.327,94 somente de juros ao banco.
Dividindo esse montante por 24 meses, você encontrará o valor da parcela, que será de R$ 846,99.
A fórmula dos juros compostos é a seguinte:
A = P (1 + i)^t
onde:
- A= valor final da operação;
- P = valor inicialmente aplicado;
- i = taxa de juros; e
- t = período da operação.
Um ponto importante, o parâmetro de tempo da taxa deve ser o mesmo do período.
Por exemplo, se a taxa é mensal, coloque o período em meses também.
Geralmente, as taxas de juros vêm expressas ao mês ou ao ano.
Neste caso, você pode utilizar um Conversor de Taxa da Juros Anual em Mensal.
Desse modo, você descobrirá qual é a taxa equivalente ao mês da taxa anual que te foi informada.
Destaques
Simuladores Financeiros








